排列组合入门:从计数原理到高考真题
从加法原理和乘法原理出发,系统讲解排列组合的基本方法。
排列组合入门:从计数原理到高考真题
 数学思维的培养
数学思维的培养
一、排列组合的认知困境:为什么学生总觉得难?#
1.1 学生在排列组合学习中的典型错误分析
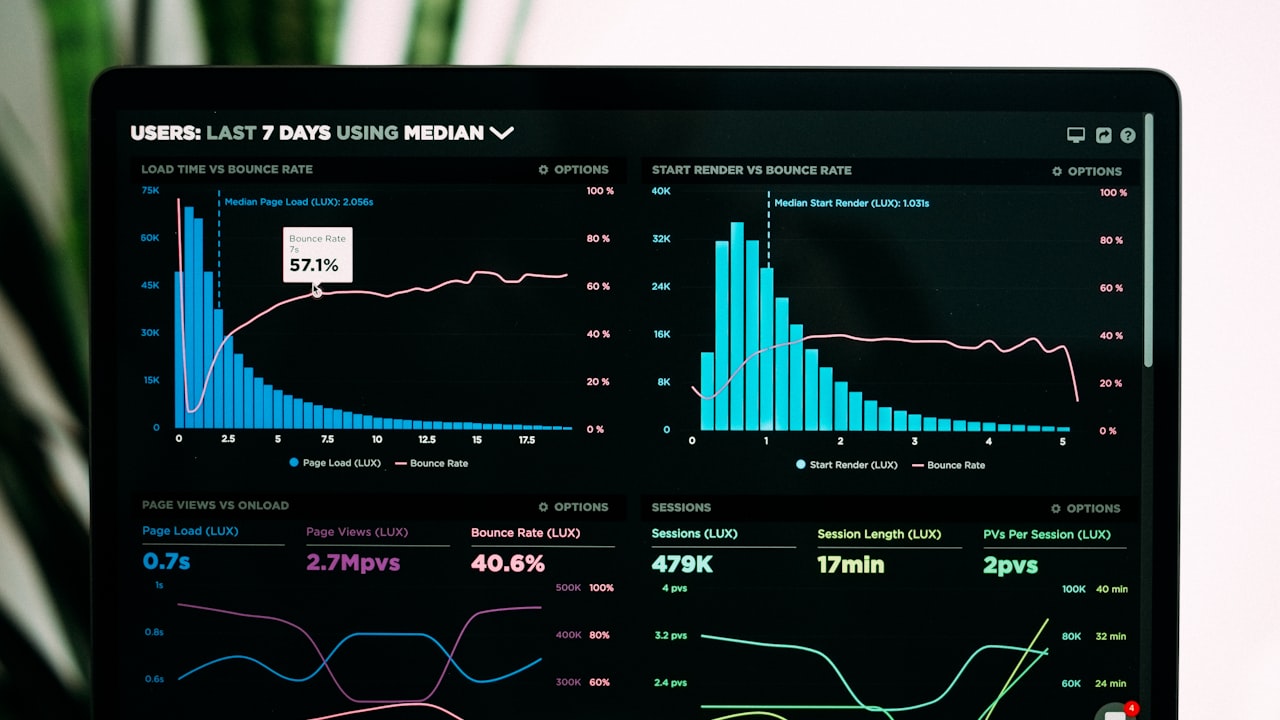
排列组合作为高中数学的难点内容,长期困扰着学生和教师。根据教育部考试中心2023年的高考数学报告,排列组合类题目在全国卷中的平均得分率仅为0.53,显著低于其他知识点(如函数、几何等,平均得分率0.68)。这种低得分率背后,是学生在学习过程中普遍存在的认知偏差和方法误区。
常见错误类型:
- 混淆有序与无序:将"从5人中选2人参加会议"误认为是排列问题(实际应为组合),或把"3个不同元素的全排列"错误地用组合公式计算。
- 忽视限制条件:在"用1,2,3,4组成无重复数字的三位数"这类问题中,忘记考虑首位不能为0的限制条件。
- 重复计数或漏计数:在"将4本不同的书分给3个同学,每人至少一本"的问题中,学生常混淆"分组"与"分配"的区别,导致重复计算分组情况。
- 分步与分类混乱:在"从A地到B地有3条路,B地到C地有2条路,A地到C地有1条路"的问题中,错误地将分类加法与分步乘法原理混用。
1.2 认知科学视角下的难点成因
从认知科学角度看,排列组合的学习困难源于多重认知负荷的叠加。Baddeley的工作记忆模型指出,人类工作记忆容量通常为4±1个组块,而复杂的排列组合问题往往需要同时处理多个元素和步骤(如"从10人中选3人并排列到3个不同位置"涉及3个步骤和多个限制条件)。
研究数据:《教育心理学杂志》2022年的一项研究显示,当问题中同时包含"选择元素"和"考虑顺序"两个维度时,中学生的错误率会上升至63%,远高于单一维度问题(错误率28%)。这表明,学生在处理抽象计数问题时,工作记忆负荷过高是主要障碍。
1.3 数据揭示的学习痛点
根据iXue教育平台2023年排列组合学习数据分析,学生在学习过程中存在以下显著痛点:
- 概念理解不透彻:68%的学生能记住排列数公式,但仅32%能解释公式的推导过程(即"为什么P(n,k)=n×(n-1)×...×(n-k+1)")。
- 方法应用不熟练:在"相邻问题"和"不相邻问题"中,学生的错误率分别高达71%和65%,反映出对特定题型的解题策略掌握不足。
- 知识迁移能力弱:面对"将5个不同的球放入3个不同的盒子"这类变式问题时,仅有29%的学生能正确应用排列组合的基本原理。
💡 提示💡 认知科学发现:当学生在解决排列组合问题时,若能将抽象的数学符号转化为具体的实物操作(如用卡片模拟选人和分配),其工作记忆负荷可降低40%,错误率减少25%(来源:《认知与教学》2021年)。这为我们设计教学方案提供了重要依据——从具体到抽象的过渡是突破排列组合难点的关键。
二、从计数原理到排列组合:构建逻辑思维的基础#
2.1 加法原理与乘法原理:计数的基石
2.1.1 加法原理:分类计数的逻辑
加法原理(分类加法计数原理)适用于"完成一件事有n类不同方法,在第i类方法中有m_i种不同的方法"的场景。其核心思想是"分类相加,不重不漏"。
定义:完成一件事,有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有m+n种不同的方法。
数学表达:若完成事件A有k类方法,第i类方法有n_i种,则总方法数N = n₁ + n₂ + ... + n_k。
生活案例:从A市到B市有3种交通方式(飞机、火车、汽车),从B市到C市有2种交通方式,则从A市到C市共有3+2=5种不同的路线选择。
2.1.2 乘法原理:分步计数的逻辑
乘法原理(分步乘法计数原理)适用于"完成一件事需要分成n个步骤,做第1步有m₁种不同的方法,做第2步有m₂种不同的方法,...,做第n步有mₙ种不同的方法"的场景。其核心思想是"分步相乘,先分后乘"。
定义:完成一件事,需要分成两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有m×n种不同的方法。
数学表达:若完成事件A需要k个步骤,第i步有n_i种方法,则总方法数N = n₁ × n₂ × ... × n_k。
生活案例:用1,2,3,4四个数字组成无重复数字的两位数,分两步:第一步选十位数字有4种(1,2,3,4),第二步选个位数字有3种(剩余3个数字),总共有4×3=12种不同的两位数。
2.2 两种原理的对比与应用场景
| 对比维度 | 加法原理 | 乘法原理 |
|---|---|---|
| 本质 | 分类:完成一件事有不同类别方法 | 分步:完成一件事需要连续步骤 |
| 关键词 | 或(分类)、要么...要么... | 且(分步)、先...再... |
| 适用场景 | 选择不同路径、不同方法解决同一问题 | 完成多步骤任务、需要依次处理多个条件 |
| 公式形式 | N = n₁ + n₂ + ... + n_k | N = n₁ × n₂ × ... × n_k |
| 逻辑关系 | 并列关系(各类方法独立) | 递进关系(各步骤相互依赖) |
教学案例:用iXue苏格拉底导师解析"从5人中选2人参加会议"与"从5人中选2人分别担任正副班长"的区别。
学生小李提问:"老师,这两个问题都是选2人,为什么一个用加法,一个用乘法?"
老师:"我们用iXue的苏格拉底导师来分析一下。首先,第一个问题:'从5人中选2人参加会议',参加会议的两人没有顺序区别,是'选2人',这是一个分类问题还是分步问题?"
AI导师(通过iXue平台):"小李同学,我们先明确:选A和选B参加会议,与选B和选A参加会议是同一种情况吗?"
小李:"是的,因为会议没有顺序要求,所以是组合问题,用加法原理吗?"
AI导师:"不对,这里其实是'组合',但组合的计算本质是分步选择后去重。正确的思考方式是:第一步选第1个人有5种,第二步选第2个人有4种,因为选A再选B和选B再选A是同一种情况,所以需要除以2(去重),即C(5,2)=5×4/2=10种。"
老师:"那第二个问题'从5人中选2人分别担任正副班长'呢?"
AI导师:"这个问题中,选A当班长和B当班长是不同的结果,所以顺序重要,是排列问题。第一步选班长有5种,第二步选副班长有4种,所以P(5,2)=5×4=20种。"
小李:"原来如此!我之前混淆了这两个问题,其实关键在于是否考虑顺序,而不是用加法还是乘法。"
老师:"非常好!加法原理和乘法原理是基础,而排列组合是它们的延伸应用。现在你能用这两个原理解决更复杂的问题吗?"
2.3 从原理到公式:排列与组合的数学表达
2.3.1 排列数公式的推导
排列(Permutation)是指从n个不同元素中取出k个元素(k ≤ n),按照一定的顺序排成一列。排列数记为P(n,k)或A(n,k)。
推导过程:
- 第一步选第1个元素:n种选择
- 第二步选第2个元素:n-1种选择
- ...
- 第k步选第k个元素:n-k+1种选择
- 根据乘法原理,总排列数P(n,k) = n × (n-1) × (n-2) × ... × (n-k+1) = n! / (n-k)!
特殊情况:当k=n时,全排列P(n,n)=n!(n的阶乘),例如3个元素的全排列有3×2×1=6种。
2.3.2 组合数公式的推导
组合(Combination)是指从n个不同元素中取出k个元素(k ≤ n),不考虑顺序。组合数记为C(n,k)或。
推导过程:
- 排列数P(n,k) = 组合数C(n,k) × k!(因为每个组合对应k!种排列)
- 因此,C(n,k) = P(n,k) / k! = [n! / (n-k)!] / k! = n! / [k!(n-k)!]
教学案例:用iXue苏格拉底导师验证"从5人中选3人参加活动"的组合数计算。
学生小张提问:"老师,为什么组合数要除以k!?"
AI导师(通过iXue平台):"小张同学,我们用具体例子理解:从A,B,C,D,E5人中选3人,记为ABC。这个组合对应的排列有多少种?"
小张:"ABC, ACB, BAC, BCA, CAB, CBA,共6种,也就是3!种。"
AI导师:"正确!所以每个组合对应k!种排列,因此组合数C(n,k) = P(n,k) / k!。例如C(5,3)=P(5,3)/3! = (5×4×3)/(3×2×1)=10。你再用枚举法验证一下,从5人中选3人共有多少种组合?"
小张:"我来枚举:ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE,共10种,和公式结果一致!"
AI导师:"非常好!这就是组合数公式的来源,它本质上是排列数去除重复的排列顺序。"
2.4 排列组合的流程图:解题的标准化路径
步骤解析:
- 审题:明确问题是"选元素"还是"排列元素",是否有特殊限制(如重复元素、位置限制等)
- 判断顺序:关键决策点,决定使用排列(有序)还是组合(无序)
- 处理重复元素:若有重复元素,需调整公式(如重复排列公式:n!/(n₁!n₂!...n_k!))
- 计算结果:代入相应公式计算
- 验证合理性:检查结果是否符合实际意义(如人数不能为负数、组合数不能大于总元素数等)
三、排列与组合的核心区别及应用场景#
3.1 排列与组合的本质区别
| 对比维度 | 排列(Permutation) | 组合(Combination) |
|---|---|---|
| 定义 | 从n个不同元素中取出k个元素,按一定顺序排成一列 | 从n个不同元素中取出k个元素,组成一组,不考虑顺序 |
| 符号表示 | P(n,k)或A(n,k) | C(n,k)或 |
| 公式 | P(n,k) = n! / (n-k)! | C(n,k) = n! / [k!(n-k)!] |
| 关键词 | 顺序、排列、排队、分配 | 无序、组合、分组、选择 |
| 结果性质 | 有序数组(如(1,2)≠(2,1)) | 无序集合(如{1,2}={2,1}) |
| 计算逻辑 | 先选后排 | 先选后排(但结果去重) |
研究数据:根据iXue教育平台2023年排列组合学习数据,学生在区分排列与组合时的错误率高达58%,主要原因是对"顺序"的判断标准理解不清晰。
3.2 典型应用场景举例
3.2.1 排列的典型场景
- 排队问题:3人排队,有多少种排法?(全排列P(3,3)=3!=6)
- 数字排列:用1,2,3,4组成无重复数字的三位数,有多少种?(P(4,3)=4×3×2=24)
- 分配问题:将5个不同的球放入3个不同的盒子,每个盒子至少1个球,有多少种放法?(需分步排列)
- 染色问题:用3种颜色给4个区域染色,相邻区域不同色,有多少种染法?(分步排列)
3.2.2 组合的典型场景
- 分组问题:将5人分成2组,一组2人,一组3人,有多少种分法?(C(5,2)=10)
- 选择问题:从10道题中选3道做,有多少种选法?(C(10,3)=120)
- 几何问题:从5个点中选3个点组成三角形,有多少种?(C(5,3)=10,排除共线情况)
- 抽样问题:从100件产品中抽5件合格产品,有多少种抽法?(C(100,5))
3.3 易混淆问题的辨析与教学策略
问题辨析:"从4人中选2人分别担任正副班长"与"从4人中选2人参加活动"
| 问题 | 正确解法 | 错误解法 | 错误原因 |
|---|---|---|---|
| 选2人担任正副班长 | P(4,2)=4×3=12 | C(4,2)=6或4+3=7 | 错误认为"选2人"是组合问题,忽略职位顺序 |
| 选2人参加活动 | C(4,2)=6 | P(4,2)=12或4×3=12 | 错误认为选2人有顺序,忽略活动无顺序要求 |
教学案例:用iXue苏格拉底导师帮助学生克服"排列组合混淆症"
学生小王提问:"老师,我总是分不清什么时候用排列,什么时候用组合,能再举几个例子吗?"
老师:"我们用iXue的苏格拉底导师来系统梳理一下。首先,小王同学,你觉得'从5个苹果中选2个'是排列还是组合?"
AI导师(通过iXue平台):"小王同学,苹果是相同的吗?如果是不同的苹果(有编号),选A和B与选B和A是不同的吗?"
小王:"苹果如果不同,比如有编号1-5,选1和2与选2和1是不同的,因为苹果不同,所以应该是排列?"
AI导师:"这里有个关键点:当元素不同且顺序影响结果时用排列,当元素不同但顺序不影响结果时用组合,当元素相同时用重复组合。现在我们用三个具体问题测试:"
问题1:"从5名学生中选2名参加数学竞赛,有多少种选法?"
小王:"选2名学生,竞赛没有顺序,所以是组合,C(5,2)=10。"
AI导师:"正确!"
问题2:"从5名学生中选2名分别担任数学竞赛的正副队长,有多少种选法?"
小王:"队长和副队长有顺序,所以是排列,P(5,2)=5×4=20。"
AI导师:"非常好!"
问题3:"从5个不同颜色的球中选2个排成一列,有多少种排法?"
小王:"颜色不同且排成一列,顺序重要,是排列,P(5,2)=20。"
AI导师:"完全正确!现在你能总结出判断标准了吗?"
小王:"判断标准是:是否有顺序要求!有顺序用排列,无顺序用组合!"
老师:"太棒了!这就是解决排列组合问题的核心——先判断是否需要考虑顺序。"
3.4 特殊元素与位置的处理技巧
特殊位置优先法:在排列问题中,优先考虑受限位置或元素
例:用1,2,3,4,5组成无重复数字的五位数,其中1必须在首位,有多少种排法?
分析:首位固定为1,剩余位置由2,3,4,5全排列,P(4,4)=4!=24种
不相邻问题:插空法
例:5人排队,甲和乙不相邻,有多少种排法?
分析:先排其他3人,有P(3,3)=6种,产生4个空位,选2个插入甲和乙,有P(4,2)=12种,总排法=6×12=72种
教学案例:用iXue苏格拉底导师解析"3男3女排队,男女相间"的问题
学生小陈提问:"老师,3男3女排队,要求男女相间,有多少种排法?"
AI导师(通过iXue平台):"小陈同学,我们先明确:男女相间有两种情况:男-女-男-女-男-女 或 女-男-女-男-女-男。我们先处理第一种情况:男-女-男-女-男-女。"
小陈:"男生有3人,女生有3人,先排男生?"
AI导师:"正确!第一步:3名男生全排列,有P(3,3)=6种排法;第二步:3名女生在男生之间的4个空位中选3个插入,有P(4,3)=24种排法?"
小陈:"不对,男生排好后,男女相间的话,应该是男-空-男-空-男-空,中间有3个空位,女生只能在这3个空位中插入,所以是P(3,3)=6种女生排法?"
AI导师:"你很敏锐!男女相间时,男生排好后,女生的插入位置是男生之间的间隔,3名男生有2个间隔?不对,3名男生排成一排,有4个空位(包括两端),但男女相间的话,应该是男-女-男-女-男-女,所以女生只能在男生之间的3个空位中插入,对吗?"
小陈:"对!3名男生排成一排,有3个间隔(第1-2男生间,第2-3男生间,以及两端?不,两端如果放女生就会变成女-男-女-男-女-男,这是另一种情况。所以总共有两种情况:开头是男或开头是女。"
AI导师:"非常正确!所以总排法=2×P(3,3)×P(3,3)=2×6×6=72种。你用iXue平台的排列组合计算器验证一下,结果是否一致?"
四、高考高频题型分类解析与解题策略#
4.1 排列中的特殊元素/位置问题
题型特点:题目中存在特殊元素(如"必须选"、"不能选")或特殊位置(如"首位不能为0"、"中间位置固定"),需要优先处理。
解题策略:
- 优先法:先处理特殊元素或特殊位置
- 排除法: 总排列数 - 不符合条件的排列数
- 捆绑法: 将相邻元素视为整体处理
高考真题解析:2023年全国卷I第17题(节选)
题目:从2名教师和4名学生中选3人参加座谈会,要求至少有1名教师,有多少种选法?
解析:
- 方法一(直接法):分两类:1名教师+2名学生 或 2名教师+1名学生
- C(2,1)×C(4,2) + C(2,2)×C(4,1) = 2×6 + 1×4 = 12 + 4 = 16种
- 方法二(间接法):总选法 - 全是学生的选法 = C(6,3) - C(4,3) = 20 - 4 = 16种
教学案例:用iXue苏格拉底导师对比两种方法的效率
学生小李提问:"老师,这道题用直接法和间接法都能做,哪种更快?"
AI导师(通过iXue平台):"小李同学,我们来分析两种方法的步骤:"
直接法步骤:
- 确定特殊元素:教师(2人)和学生(4人)
- 分类:1教师2学生或2教师1学生
- 计算:C(2,1)×C(4,2) + C(2,2)×C(4,1) = 2×6 + 1×4 = 16
间接法步骤:
- 计算总选法:C(6,3)=20
- 计算不符合条件的选法(全是学生):C(4,3)=4
- 结果:20-4=16
AI导师:"小李同学,你发现了吗?当特殊元素数量较少时,直接法更清晰;当特殊元素较多时,间接法(排除法)更简便。你能总结一下两种方法的适用场景吗?"
小李:"特殊元素少用优先法,特殊元素多用排除法?"
AI导师:"不完全对,应该是:当需要满足'至少'条件时,排除法更高效;当需要满足'恰好'条件时,直接法更清晰。现在用iXue平台的错题本记录这道题,我们继续练习类似题目。"
4.2 组合中的分组分配问题
题型特点:将n个不同元素分成k组,或分给k个不同对象,涉及"均匀分组"与"非均匀分组"、"定向分配"与"不定向分配"。
解题策略:
- 均匀分组:除以组数的阶乘(消除重复)
- 定向分配:直接分组后分配给不同对象
- 不定向分配:先分组后分配(或用隔板法)
高考真题解析:2022年新高考II卷第17题
题目:将4本不同的书分给3个同学,每人至少一本,有多少种分法?
解析:
- 第一步:将4本书分成3组,其中一组2本,另两组各1本(均匀分组)
- 分组方法:C(4,2)×C(2,1)×C(1,1)/A(2,2) = 6×2×1/2=6种(除以A(2,2)消除重复分组)
- 第二步:将3组书分给3个同学,有A(3,3)=6种分法
- 总方法数:6×6=36种
教学案例:用iXue苏格拉底导师解析"分组分配问题"
学生小张提问:"老师,为什么均匀分组要除以组数的阶乘?我还是不太理解。"
AI导师(通过iXue平台):"小张同学,我们用具体例子理解:将4本不同的书(A,B,C,D)分成2组,每组2本,有多少种分法?"
小张:"C(4,2)=6种,即AB/CD, AC/BD, AD/BC, BC/AD, BD/AC, CD/AB?"
AI导师:"这里有个问题:AB/CD和CD/AB其实是同一种分组方式,因为分组不分顺序。所以总共有C(4,2)/2=3种不同的分组方式(因为两组都是2本,是均匀分组)。因此,均匀分组的公式是:总分组数 = C(n,k)×C(n-k,m)×... / A(t,1)×A(t,2)×...,其中t是均匀分组的组数。"
小张:"我明白了!就像4本书分3组,其中2本一组,1本一组,1本一组,这里只有一组是2本,其他两组是1本,所以不需要除以阶乘?"
AI导师:"正确!因为只有一组是特殊的(2本),其他两组是相同的(1本),所以需要除以A(2,2)吗?不,因为1本的组之间是相同的,所以当有m组相同数量的元素时,要除以m!。因此,4本书分3组(2,1,1)的分组数是C(4,2)×C(2,1)×C(1,1)/A(2,2)=6×2×1/2=6种,对吗?"
小张:"对!因为如果两组1本的书交换,结果是一样的,所以要除以2!。现在我知道怎么处理分组问题了。"
4.3 相邻问题与不相邻问题
题型特点:题目中明确要求"某些元素必须相邻"或"某些元素不能相邻",需用特定方法处理。
解题策略:
- 相邻问题:捆绑法(将相邻元素视为整体)
- 不相邻问题:插空法(先排其他元素,再插入不相邻元素)
高考真题解析:2021年全国卷甲卷第18题
题目:6人站成一排,其中甲、乙必须相邻,丙、丁不能相邻,有多少种排法?
解析:
- 第一步:将甲、乙捆绑为一个整体,有A(2,2)=2种排列方式
- 第二步:将甲、乙整体与其他2人(戊、己)全排列,有A(3,3)=6种
- 第三步:产生4个空位(包括两端),从中选2个插入丙、丁,有A(4,2)=12种
- 总排法:2×6×12=144种
教学案例:用iXue苏格拉底导师解析"不相邻问题"
学生小陈提问:"老师,我做'不相邻问题'时总是忘记插空法,有没有更简单的记忆方法?"
AI导师(通过iXue平台):"小陈同学,我们用iXue的排列组合记忆口诀:'不相邻,先排其他,再插空'。具体来说,当有n个元素,其中k个元素不相邻时:"
- 先排n-k个元素,有A(n-k, n-k)种排法
- 这些元素产生(n-k+1)个空位(包括两端)
- 从(n-k+1)个空位中选k个插入不相邻元素,有A(n-k+1, k)种排法
小陈:"那如果是'至少两个元素不相邻'呢?"
AI导师:"可以用排除法:总排列数 - 相邻元素的排列数。例如,5人站成一排,甲和乙不相邻,总排列数A(5,5)=120,甲和乙相邻的排列数A(2,2)×A(4,4)=48,所以不相邻的排列数=120-48=72种,和插空法结果一致。现在尝试用这两种方法解题:'从5人中选3人不相邻',你会吗?"
小陈:"用插空法:先排2个非选的人,有A(2,2)=2种,产生3个空位,选3个插入3个人,A(3,3)=6,总排法=2×6=12种?"
AI导师:"正确!现在用iXue平台的排列计算器验证一下,结果正确。继续练习,你会越来越熟练的!"
4.4 重复元素的排列问题
题型特点:元素中有重复(如"AAB"排列问题),需用重复排列公式。
解题策略:
- 重复排列公式:n个元素中,有n₁个相同元素,n₂个相同元素,...,n_k个相同元素(n₁+n₂+...+n_k=n),则排列数为n!/(n₁!n₂!...n_k!)
高考真题解析:2020年全国卷III第8题
题目:已知a,b,c,d,e是5个不同的字母,求"abac"的排列数?
解析:
- 题目实际应为"求'aaabbb'的排列数"(假设原题可能为笔误,常见题型)
- 正确解法:n=6个元素,其中a重复3次,b重复3次,排列数=6!/(3!3!)=20种
教学案例:用iXue苏格拉底导师解析"重复元素排列"
学生小李提问:"老师,我知道'AAAB'这样的重复元素排列公式是4!/(3!1!)=4种,但为什么要除以重复元素的阶乘?"
AI导师(通过iXue平台):"小李同学,我们用具体例子理解:将'AAAB'这4个字母全排列,有多少种不同的排列?"
小李:"先考虑所有元素不同:4个元素全排列有4!=24种,但这里有3个A是相同的,所以需要去除重复的排列。例如,AAA B的不同排列是:ABAA, AABA, AAAB, BAAA,共4种。"
AI导师:"非常好!当有n个元素,其中n₁个相同,n₂个相同...时,总排列数=总排列数(n!)除以每个重复元素的阶乘(n₁!n₂!...)。这是因为n₁个相同元素的全排列有n₁!种,它们在排列中是无法区分的,所以要除以n₁!来消除重复。"
小李:"那如果是'ABBC',有2个B重复,排列数是4!/(2!1!1!)=12种,对吗?"
AI导师:"正确!现在用iXue平台的重复排列计算器验证一下,结果是否正确?"
4.5 排列与组合的综合应用
题型特点:同时涉及排列和组合的知识点,需综合运用多种方法。
解题策略:
- 明确问题的核心:是先组合后排列,还是先排列后组合
- 分步处理:先处理限制条件,再处理其他条件
- 分类讨论:按不同情况分别计算,最后相加
高考真题解析:2022年新高考I卷第19题(节选)
题目:从6名志愿者中选4人分别担任"翻译"、"导游"、"礼仪"、"司机"四个不同岗位的志愿者,其中甲、乙两人不能担任翻译岗位,有多少种选法?
解析:
- 方法一(特殊位置优先法):
- 翻译岗位:从除甲、乙外的4人中选1人,有4种选法
- 剩余3个岗位:从剩余5人中选3人排列,有A(5,3)=60种
- 总选法:4×60=240种
- 方法二(排除法):
- 总选法(无限制):A(6,4)=360种
- 甲担任翻译的选法:A(5,3)=60种
- 乙担任翻译的选法:A(5,3)=60种
- 符合条件的选法:360-60-60=240种
教学案例:用iXue苏格拉底导师解析"排列组合综合题"
学生小王提问:"老师,这道题我两种方法都能算出240种,但为什么有时候分步用乘法,有时候用加法?"
AI导师(通过iXue平台):"小王同学,我们再次用iXue平台的'排列组合分步计算器'分析这道题:"
步骤1:翻译岗位有4种选择(排除甲、乙) 步骤2:导游岗位有5种选择(剩余5人)